Calculating an Average Infant Mortality Factor Over a Given Service Life Using the 217Plus™ Methodology
Infant mortality is a term that is often used to describe early-life failures – that is, failures that occur due to premature excitation of failure mechanisms. Such failures are typically due to inferior material (e.g., parts used in the manufacturing process that are out of tolerance), poor workmanship due to inadequate skills being used in manufacturing, improper installation or other quality problems. All hardware is released into service with infant mortality defects (also known as latent defects). As the hardware is used, operational and environmental stresses precipitate these latent defects in the form of failures. The failures are then corrected through repair or rework (hopefully without the introduction of new defects), and the hardware is returned to service. Although infant mortality failures can occur at any time during the life cycle of the hardware, they tend to be concentrated during early life. Thus, as these failures are repaired, the number of infant mortality defects remaining decreases and the hardware components that remain have longer lifespans. Therefore, during the early life period, the instantaneous failure rate of the hardware tends to decrease with time. This process can be accelerated through the performance of Environmental Stress Screening (ESS) prior to delivery to the customer. In this way, a greater percentage of infant mortality defects are precipitated and removed from the hardware prior to entry into service, resulting in a lower instantaneous failure rate.
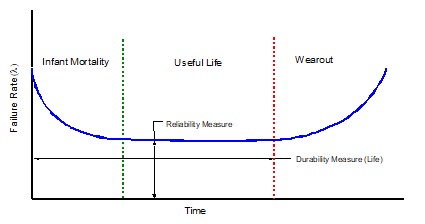
Figure 1: Bathtub Curve
The 217PlusTM methodology, initially developed by Quanterion under the DoD Reliability Information Analysis Center (RIAC), and subsequently updated by Quanterion to 217PlusTM:2015 and 217PlusTM:2015, Notice 1 after the RIAC ceased operations in 2014, considers infant mortality in its system failure rate prediction model.
The 217PlusTM system failure rate model is as follows 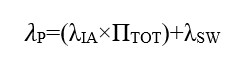
Where![]()
λP is the overall system failure rate in failures per million calendar hours.
λIA is the summed failure rate of the components (capacitors, resistors, ICs, etc.) of the system. It is calculated using the 217PlusTM failure rate models, values from Non-Electronic Part Reliability Database 2016 (NPRD-2016), field performance, etc.
∏TOT is the overall process grade factor that is applied to the summed component failure rate to arrive at the system failure rate. It is calculated from an assessment of the strength of a manufacturer’s processes in the following areas: systems management, design engineering, manufacturing, parts quality, induced failures, cannot duplicate (CND) incidents, wear-out, reliability growth and infant mortality. Also included is an environmental factor, which is a function of the operating and non-operating temperature, along with relative humidity and vibration level. The individual ∏ factors (with the exceptions of ∏E and ∏IM) are calculated by performing a process grade assessment. If a process grade assessment has not been performed, default parameters representing an average process can be used. ∏E is calculated from the environmental parameters.
λSW is the software failure rate.
Infant mortality is accounted for in the Quanterion 217PlusTM methodology with a time-variant factor that is a function of the expected effectiveness of the applied ESS. The infant mortality factor, ![]() , is calculated as:
, is calculated as:
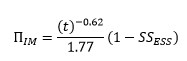
In this expression, “t” is the time (in years) at which infant mortality of the system is to be assessed after it enters into service (representing the time at which the instantaneous system failure rate is to be calculated). The default value is 5 months (i.e., 0.4167 years). The term SSESS is the screening strength of the applied temperature and vibration screens. If ESS is not applied, then SSESS is set equal to 0. If ESS is applied, then the value of SSESS is calculated using the method described in the Quanterion Solutions’ “Handbook of 217PlusTM Reliability Prediction Models” (HDBK-217Plus:2015, Notice 1). For a further discussion of the screening strength methodology, refer to MIL-HDBK-344.
Given the time-variant nature of ![]() , the resulting system model presented above actually represents the instantaneous failure rate. That is, it represents the failure rate at the particular instant in time, t, given that the hardware has survived up until that point. Therefore,
, the resulting system model presented above actually represents the instantaneous failure rate. That is, it represents the failure rate at the particular instant in time, t, given that the hardware has survived up until that point. Therefore, ![]() , and hence the system failure rate, are time-dependent. As the value of “t” increases, the value of
, and hence the system failure rate, are time-dependent. As the value of “t” increases, the value of ![]() , and hence the system failure rate, decreases. This is to be expected since as the system is used, infant mortality defects are detected and removed from the population.
, and hence the system failure rate, decreases. This is to be expected since as the system is used, infant mortality defects are detected and removed from the population.
While the behavior of ![]() , and hence the system failure rate, over time is not unexpected, the selection of “t” is somewhat arbitrary. One way to remove this arbitrary selection for “t” (and remove the time dependency of the failure rate calculation) would be to calculate the “average” failure rate of the system over its service life. This approach would require the calculation of the average value of
, and hence the system failure rate, over time is not unexpected, the selection of “t” is somewhat arbitrary. One way to remove this arbitrary selection for “t” (and remove the time dependency of the failure rate calculation) would be to calculate the “average” failure rate of the system over its service life. This approach would require the calculation of the average value of ![]() over the service life of the equipment. This can be achieved by integrating the expression above with respect to time over the service life and dividing the result by the service life.
over the service life of the equipment. This can be achieved by integrating the expression above with respect to time over the service life and dividing the result by the service life.
![]() is then calculated as:
is then calculated as:
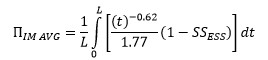
In this expression, “L” is the service life of the system in years. Performing the integration yields:
![]()
where “L” is the service life in years.
Another approach to the determination of the average value of ![]() is to calculate the value of “t” that would result in a value of
is to calculate the value of “t” that would result in a value of ![]() that would be equal to the value obtained from the integration. This approach is useful if the 217PlusTM calculation tool (such as the 217PlusTM:2015, Notice 1 Calculator) does not explicitly provide for the integration. Specifically, the value of “t” must be calculated such that:
that would be equal to the value obtained from the integration. This approach is useful if the 217PlusTM calculation tool (such as the 217PlusTM:2015, Notice 1 Calculator) does not explicitly provide for the integration. Specifically, the value of “t” must be calculated such that:
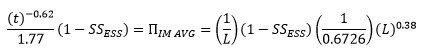
Solving for “t” yields:
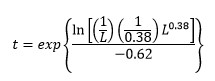
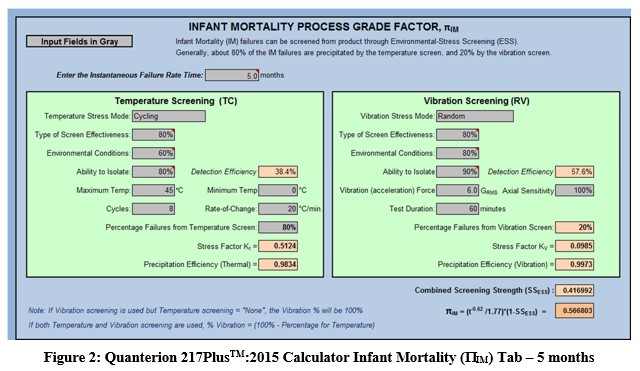
For example, consider an ESS process that applies temperature cycling and random vibration as shown in Figure 2. The screening strength, SSESS, is calculated as 0.416992. The default value of ![]() at 5 months (0.4167 years) is then calculated as (refer to Figure 2):
at 5 months (0.4167 years) is then calculated as (refer to Figure 2):
![]()
Next, suppose that we wish to calculate the average value of ![]() over a service life of 20 years using the same screening strength. One method of accomplishing this task would be to substitute the SSESS and the service life, L, in the integrated
over a service life of 20 years using the same screening strength. One method of accomplishing this task would be to substitute the SSESS and the service life, L, in the integrated ![]() equation as follows:
equation as follows:
![]()
However, since the Quanterion 217PlusTM:2015, Notice 1 Calculator does not contain the integrated equation, ![]() must be calculated using the equivalent value of “t” as follows:
must be calculated using the equivalent value of “t” as follows:
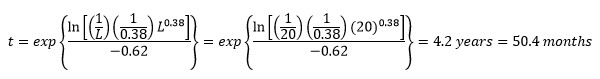
Evaluating ![]() at 4.2 years (50.4 months) yields the following (refer to Figure 3):
at 4.2 years (50.4 months) yields the following (refer to Figure 3):
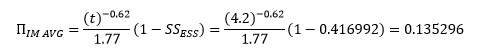
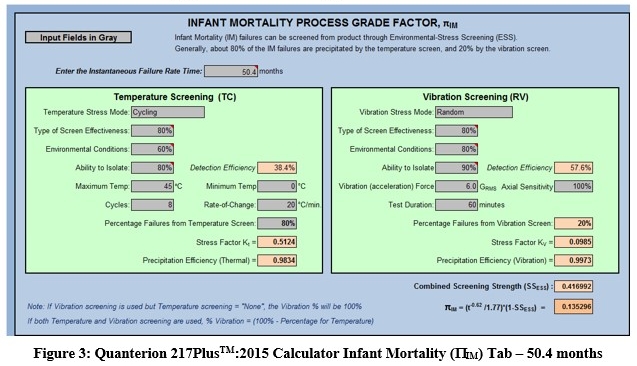
As shown above, since the average value of ![]() over a service life of 20 years would be equal to
over a service life of 20 years would be equal to ![]() evaluated at t=4.2 years or 50.4 months, users of the Quanterion 217PlusTM:2015, Notice 1 Calculator would enter 50.4 months on the ‘Infant Mortality’ tab (See Figure 3).
evaluated at t=4.2 years or 50.4 months, users of the Quanterion 217PlusTM:2015, Notice 1 Calculator would enter 50.4 months on the ‘Infant Mortality’ tab (See Figure 3).
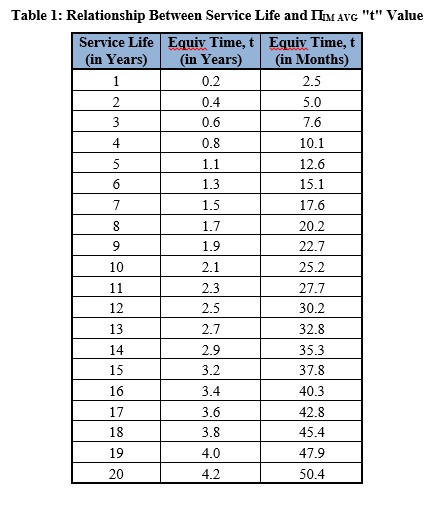
Note that the equivalent value of “t” is only dependent upon the service life. It is independent of the screening strength. A table cross referencing the service life to the value of “t” that would calculate the ![]() over that service life is shown in Table 1.
over that service life is shown in Table 1.
The value of “t” that would calculate the ![]() over a particular service life is approximately equal to 21% of the service life. Therefore, if the user wishes to calculate an average infant mortality failure rate over a given service life, the user should multiply the service life by 21% and enter that value (in months) in the ‘Infant Mortality’ tab of the Quanterion 217PlusTM:2015, Notice 1 Calculator.
over a particular service life is approximately equal to 21% of the service life. Therefore, if the user wishes to calculate an average infant mortality failure rate over a given service life, the user should multiply the service life by 21% and enter that value (in months) in the ‘Infant Mortality’ tab of the Quanterion 217PlusTM:2015, Notice 1 Calculator.